【本篇報導由物理學系Fernandes Karan Savio Arthur博士後研究員研究團隊提供】
「軟光子定理」（亦稱低能光子定理），描述了包含光子的散射振幅在光子能量極低的極限下的因子分解。最近，由於低能定理與平直時空中的邊界對稱性及可觀測量的關聯低能定理引起了新的關注。然而，低能定理在彎曲時空中的存在性及性質尚不清楚。在本文中，研究探討在具有負宇宙學常數的反德西特時空（AdS）中的散射過程。雖然這通常是非常困難的，但反德西特時空具有一個稱為「AdS/CFT對偶性」的性質，該對偶性將AdS內部的物理與AdS邊界上的量子場論的物理聯繫起來。利用這一性質，研究團隊使用了邊界量子場論中的守恆定律，即「沃德恆等式」（Ward identity），來推導出在AdS內部的散射過程中的低能因子。本研究推導出了具有宇宙學常數修正的低能光子因子，該因子包含了粒子在AdS中傳播的資訊。這一推導首次揭示了低能因子確實會受到此類修正，並理解低能定理如何推廣至非平直時空提供了新的視角。
散射振幅是量子物理中明確定義的可觀測量，用於描述粒子的散射過程。雖然散射振幅通常與高能散射事件相關，但它們在低能區域亦展現出明確的行為，並由低能定理（又稱「軟定理」soft theorems）加以描述。這些定理指出，當其中一個出射粒子是低能光子（光的量子）或低能引力子（重力的量子）時，散射振幅將因應產生一個低能因子（也稱為「軟因子」），其中蘊含了低能光子或低能引力子與其他粒子之間相互作用的資訊。平直時空中主導低能因子的表達式是由著名科學家史蒂芬·溫伯格（Steven Weinberg）數十年前推導出來的。近年來，由於低能因子與時空邊界上的漸近對稱性及守恆定律的等價性被確立，低能因子再次成為研究焦點。
上述討論主要針對平直時空，研究團隊則關注這些結果如何推廣到彎曲時空。為了討論這一點，研究團隊考慮了具有負宇宙學常數的「反德西特時空」（AdS）。反德西特時空在高能物理界中具有特殊的意義，因其內部與邊界之間存在一種對應關係。簡單來說，反德西特時空內部的物理過程可以通過位於其邊界的量子場論來等價描述。換言之，邊界量子場論的相關函數可以與定義於反德西特時空內部的散射過程相關聯，而這在平直時空中則較難計算。
研究團隊探討了具有小宇宙學常數的反德西特時空中的散射過程。這提供了平直時空低能因子的宇宙學常數修正。藉由運用邊界量子場論中的守恆定律，即「沃德恆等式」（Ward identity），推導出了具有宇宙學常數修正的低能光子因子（如圖1）。研究結果首次確立了溫伯格推導的低能因子在具有宇宙學常數的時空中存在這樣的修正。
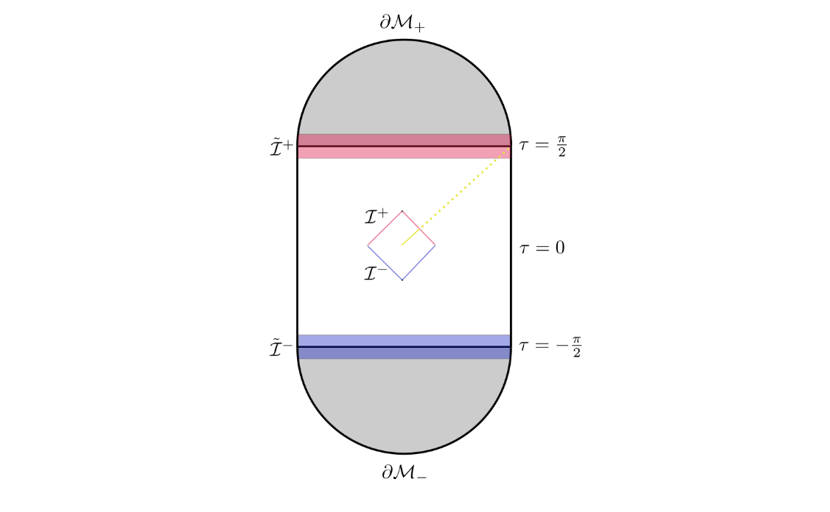
圖1：在AdS時空（膠囊形圖示）內顯示一個平坦時空區域（菱形）。平坦區域中的散射會發出輻射（黃線），該輻射會延伸至AdS時空本體（虛線）。利用AdS/CFT對應，可以在AdS邊界上使用沃德恆等式來描述平坦時空散射的軟定理。當輻射在AdS本體（虛線）中傳播時，它會對已知的平坦時空結果進行修正，並透過AdS/CFT對應為我們提供一種全息理解。
原文出處：Banerjee, N., Fernandes, K. & Mitra, A. 1/L2 corrected soft photon theorem from a CFT3 Ward identity. J. High Energ. Phys. 04, 055 (2023). https://doi.org/10.1007/JHEP04(2023)055
費爾南德斯博士於2019年在印度薩蒂恩德拉·納特·博斯基礎科學國家中心（Satyendra Nath Bose National Centre for Basic Sciences）獲得理論物理學博士學位。此後，他曾在哈里什·昌德拉研究所（Harish-Chandra Research Institute）（2019-2021）和國立臺灣大學（2021-2022）擔任博士後研究職位。自2022年8月起，他成為國立臺灣師範大學物理系的博士後研究員，並加入林豐利教授的研究團隊。 費爾南德斯博士目前的研究方向是從低能經典極限的散射振幅中推導引力波的性質。他的其他研究興趣包括「全息性」領域，該領域描述了時空內部物理與時空邊界物理之間的對應關係。這個框架為我們提供了理解量子引力的最佳視角，而量子引力仍然是理論物理中的一個未解問題。
